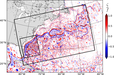
Topographic control of the Gulf Stream

North Atlantic Gyre Balance

The aim is to understand how topography influences the path and shape of the Gulf Stream, especially through bottom pressure forces, and to propose parameterizations of these mechanics for ocean general circulation models [1] [2].

The full barotropic vorticity balance equation of the flow is obtained by integrating the momentum equations in the vertical and cross differentiating them:

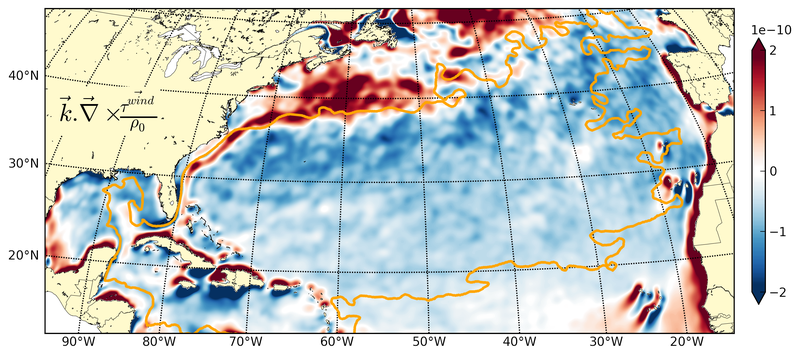
(∂Ω)/(∂t)_\rmrate = − ∇⃗.(fu⃗)_{\rmplanet. vort. adv.} + (J(P_b, h))/(ρ₀)_{\rmbot. pres. torque} + k⃗.∇⃗ × (τ⃗^wind)/(ρ₀)_{\rmwind curl} − k⃗.∇⃗ × (τ⃗^bot)/(ρ₀)_{\rmbot. drag curl} + D_Σ_{\rmhoriz.diffusion.} − A_Σ_{\rmNL advection}

Wind stress curl k⃗.∇⃗ × (τ^wind⃗)/(ρ₀).

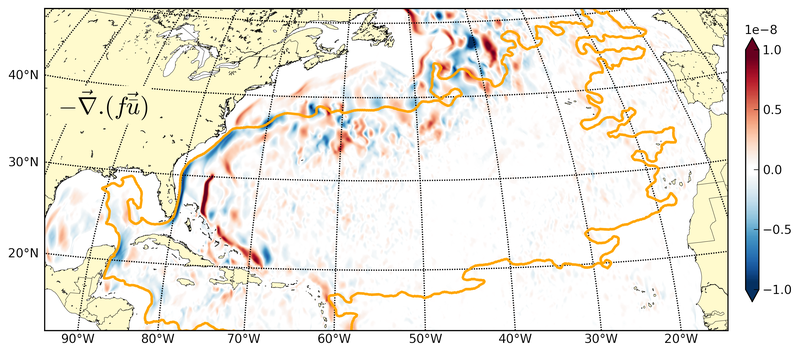
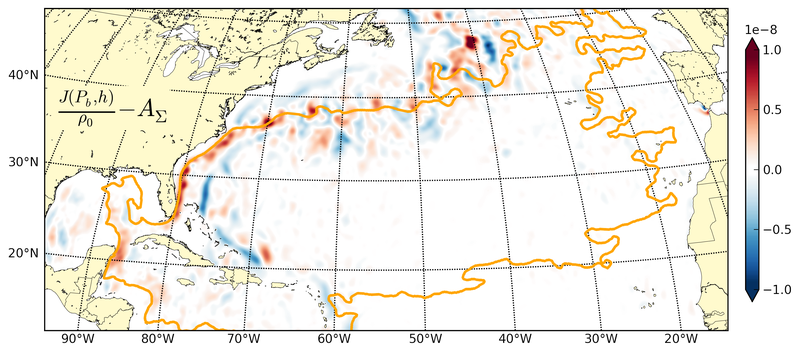
Units are m s$^{-2}$. The orange contour shows the $\Psi=0$ Sv streamfunction used to define the gyre as the largest closed contour.

By revisiting the classic gyre equilibrium problem, the dominant role of bottom pressure torque in the closure of the gyre scale barotropic vorticity budget has been established. The bottom pressure torque is the term balancing the negative input by anticyclonic wind curl on the scale of the subtropical gyre.

Local Balance in a Western Boundary Current

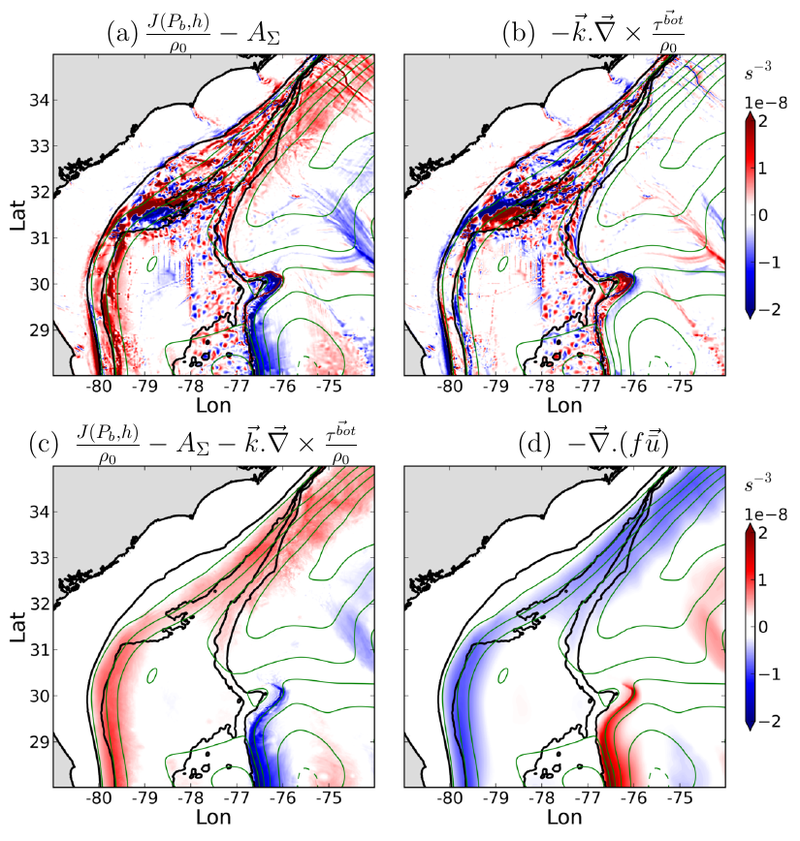
The topographic impact of the shelf provides, through bottom pressure torque, the positive input of barotropic vorticity necessary to balance the meridional transport of the planetary vorticity gradient and help close the gyre scale vorticity balance.

Bibliography

[1]	J. Schoonover, W. Dewar, N. Wienders, J. Gula, J.C. McWilliams, M.J. Molemaker, S. Bates, G. Danabasoglu & S. Yeager (2015) North Atlantic Barotropic Vorticity Balances in Numerical Models J. Phys. Oceanogr., 46, 289-303.

[2]	J. Gula, J. Molemaker and J.C. McWilliams (2015) Gulf Stream dynamics along the U.S. Eastern Seaboard. J. Phys. Oceanogr., 45, 690-715.